Bảng công thức tính tích phân, đạo hàm, nguyên hàm và những sai lầm thường gặp khi làm bài
Bảng công thức tính tích phân, đạo hàm, nguyên hàm và những sai lầm, lưu ý cần nắm khi làm bài. Trong bộ môn Toán ở trung học phổ thông thì “tích phân” là dạng toán khó và rất dễ sai. Tích phân thường xuất hiện trong các đề thi tốt nghiệp và đại học nên việc ghi nhớ những công thức tính tích phân đối với học sinh là điều hết sức quan trọng.
Vì công thức của nó rất dài nên hầu hết các em đều khó ghi nhớ, hay nhớ nhầm công thức dẫn đến lời giải bài toán sai, ảnh hưởng đến điểm số.
Băn khoăn không biết nhớ công thức như thế nào cho đúng là tâm trạng của rất nhiều học sinh lúc này. Nhưng các em đừng quá lo lắng nhé! Chúng tôi sẽ cung cấp cho các em một bảng tổng hợp các công thức tính tích phân rất dễ nhớ và hiệu quả. Hãy cùng tham khảo ngay nào!
MỘT SỐ LƯU Ý KHI LÀM TÍCH PHÂN
Hầu hết học sinh khi học thuộc hết công thức đều thấy tự tin vận dụng làm bài tập. Tuy nhiên tích phân là một dạng toán khó, ứng với mỗi bài toán để không mắc phải sai lầm, các em phải biết vận dụng linh hoạt định nghĩa, các tính chất cùng với phương pháp tính tích phân. Nhưng thực tế cho thấy, đa số học sinh tính tích phân một cách máy móc.
Sau đây là những lỗi sai các em thường mắc phải khi giải toán tích phân. Hãy chú ý và khắc phục ngay nhé!
1. Tính nguyên hàm sai, hiểu sai bản chất công thức, nhớ nhầm công thức:
Đây là lỗi đơn giản nhất mà các em thường mắc phải khi giải toán tích phân.
Các em muốn khắc phục thì ngay bây giờ:
+ Hãy học thuộc bảng nguyên hàm các hàm số cơ bản.
+ Thường xuyên tự kiểm tra công thức: Lấy đạo hàm của nguyên hàm tìm được xem có bằng hàm số đã cho.
+ Học thuộc nguyên hàm hàm hợp tương ứng với hàm số cơ bản, tự lập ra bảng nguyên hàm của hàm hợp ứng với u = ax+b

* Các em cần chú ý:
Khi tính 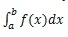 cần chú ý xem hàm số y = f(x) có liên tục trên [a; b] không? nếu có thì áp dụng phương pháp đã học để tính tích phân đã cho còn nếu không thì kết luận ngay tích phân này không tồn tại.
cần chú ý xem hàm số y = f(x) có liên tục trên [a; b] không? nếu có thì áp dụng phương pháp đã học để tính tích phân đã cho còn nếu không thì kết luận ngay tích phân này không tồn tại.
2. Lời giải sai do nhớ nhầm tính chất tích phân:
+ Học thuộc các tính chất của nguyên hàm và tích phân.
+ Tổng quát hóa các dạng toán sử dụng phương pháp tích phân từng phần.
3. Sai lầm khi đổi biến số:
+ Học thuộc các bước thực hiện phương pháp đổi biến số
+ Kiểm tra kết quả bằng phép tính gần đúng trên máy tính bỏ túi.

Do tan(π/2) không xác định nên tích phân trên không tồn tại
*Nguyên nhân sai của các em nè:
Đặt t = tan(x/2) ∈ [0; π] tại x = π thì tan(x/2) không có nghĩa.
* Các em cần lưu ý:
Đối với phương pháp đổi biến số khi đặt t = u(x) thì u(x) phải là một hàm số liên tục và có đạo hàm liên tục trên [a; b].
4. Sai lầm vì dùng công thức không có trong sách giáo khoa:
+ Ghi nhớ công thức cách chứng minh một số công thức nguyên hàm mở rộng.
+ Khi gặp tích phân mở rộng thì không được áp dụng thẳng mà phải chứng minh trước rồi mới sử dụng.
5. Hiểu sai bản chất công thức cũng là nguyên nhân làm lời giải sai:
+ Với từng công thức, từng kí hiệu trong công thức phải nắm thật kỹ
+ Làm thật nhiều ví dụ để ghi nhớ lâu công thức, tránh nhầm lẫn.
Tích phân là kiến thức vô cùng mới mẻ đối với hầu hết học sinh. Do đó khi học vừa đạo hàm, nguyên hàm, tích phân các em rất dễ nhầm lẫn. Ta có thể dựa vào công thức đạo hàm để hình thành nguyên hàm, nhưng không thể sử sụng đạo hàm cho tích phân. Hãy cẩn thận áp dụng công thức cho phù hợp các em nhé! Chúc các em có kết quả thật tốt trong học tập.
Nguồn:
- Cảm nhận về bức tranh thiên nhiên mùa hè trong bài thơ Cảnh Ngày Hè của Nguyễn Trãi (13/10) Nguồn:
- Phân tích bài thơ Thuật Hoài (Tỏ Lòng) của Phạm Ngũ Lão (13/10) Nguồn:
- Phân tích nhân vật Chí Phèo và 3 lần Chí đến nhà Bá Kiến trong truyện Chí Phèo (27/09) Nguồn:
- Phân tích bi kịch tinh thần trong tác phẩm Đời Thừa của Nam Cao (27/09) Nguồn:
- Phân tích tác phẩm Hạnh phúc của một tang gia của Vũ Trọng Phụng (27/09) Nguồn:






 Từ sân bay Huế đi La Vang như thế nào?
Từ sân bay Huế đi La Vang như thế nào?
 Soạn bài Đại cáo bình Ngô của Nguyễn Trãi
Soạn bài Đại cáo bình Ngô của Nguyễn Trãi
 Phân tích bài thơ Bạch Đằng Giang Phú của Trương Hán Siêu
Phân tích bài thơ Bạch Đằng Giang Phú của Trương Hán Siêu
 Phân tích bài thơ Độc Tiểu Thanh kí của Nguyễn Du
Phân tích bài thơ Độc Tiểu Thanh kí của Nguyễn Du











